【C#】3D空間上での三角形と直線の交差判定

今回は、3D空間上での三角形（ポリゴン）と直線の交差判定のプログラムをC#で書いたのでご紹介したいと思います。3Dゲームの当たり判定やレイトレーシングなどの処理を使用できるかと思います。

使用した環境

  • Windows 10 Pro 1903 (build 18362.592)
  • Microsoft Visual Studio Community 2019 Version 16.4.2
  • .Net Framework 4.6

概要

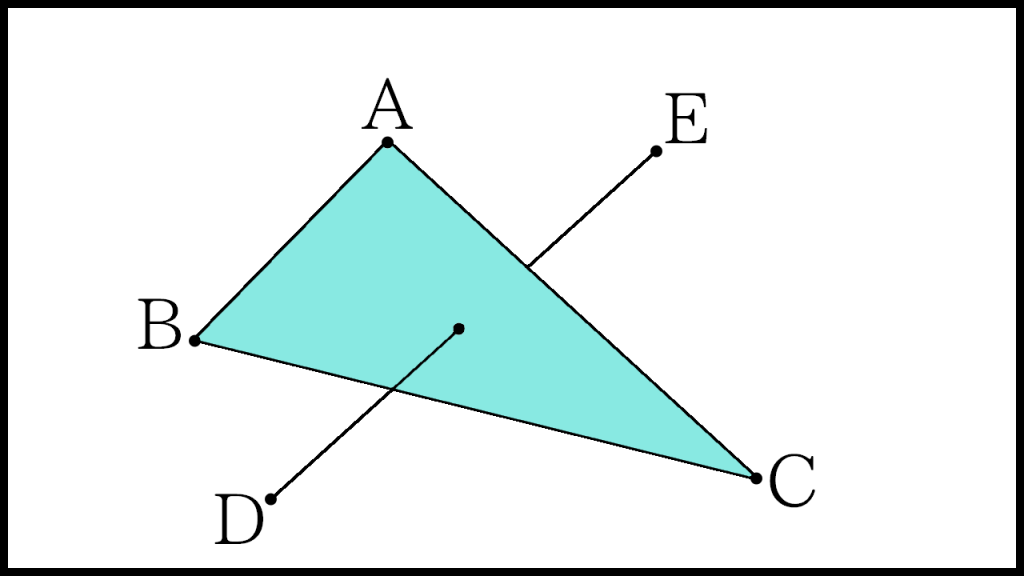
下記画像のような三角形ABCと直線DEが交差するか判定するプログラムをご紹介します。

3D空間上での三角形と直線の交差判定 概要

ソースコード

/// <summary>
/// アプリケーションのメイン エントリ ポイントです。
/// </summary>
[STAThread]
static void Main()
{
    // 交差確認①
    {
        // 三角形の頂点設定
        Vector3 vA = new Vector3(-13.01f, 14.29f, -6.99f);
        Vector3 vB = new Vector3(9.17f, 13.53f, 5.36f);
        Vector3 vC = new Vector3(-8.19f, 3.88f, -2.81f);

        // 直線の頂点設定
        Vector3 vD = new Vector3(0.9f, 16.35f, 9.03f);
        Vector3 vE = new Vector3(-4.4f, 3.68f, -7.39f);

        // 交差するか確認
        if(IsCrossTriAndLine(vA, vB, vC, vD, vE))
        {
            // 交差座標取得
            Vector3 vCross = GetCrossPointTriAndLine(vA, vB, vC, vD, vE);
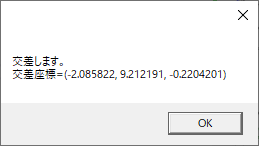
            MessageBox.Show(string.Format("交差します。\n交差座標=({0}, {1}, {2})", vCross.X, vCross.Y, vCross.Z));
        }
        else
        {
            MessageBox.Show("交差しません。");
        }
    }

    // 交差確認②
    {
        // 三角形の頂点設定
        Vector3 vA = new Vector3(0.9f, 16.35f, 9.03f);
        Vector3 vB = new Vector3(-4.4f, 3.68f, -7.39f);
        Vector3 vC = new Vector3(10.17f, -5.0f, 0.0f);

        // 直線の頂点設定
        Vector3 vD = new Vector3(-11.45f, 11.69f, -5.6f);
        Vector3 vE = new Vector3(8.8f, 31.03f, -0.42f);

        // 交差するか確認
        if (IsCrossTriAndLine(vA, vB, vC, vD, vE))
        {
            // 交差座標取得
            Vector3 vCross = GetCrossPointTriAndLine(vA, vB, vC, vD, vE);
            MessageBox.Show(string.Format("交差します。\n交差座標=({0}, {1}, {2})", vCross.X, vCross.Y, vCross.Z));
        }
        else
        {
            MessageBox.Show("交差しません。");
        }
    }
}

/// <summary>
/// 三角形と直線が交差するか判定
/// </summary>
/// <param name="vA"></param>
/// <param name="vB"></param>
/// <param name="vC"></param>
/// <param name="vD"></param>
/// <param name="vE"></param>
/// <returns></returns>
private static bool IsCrossTriAndLine(Vector3 vA, Vector3 vB, Vector3 vC, Vector3 vD, Vector3 vE)
{
    bool bRet = false;
    try
    {
        float[] fAry = GetCrossJudgeParam(vA, vB, vC, vD, vE);
        if (fAry != null)
        {
            float k = fAry[0];
            float l = fAry[1];
            float d = fAry[2];

            if (0 <= k && k <= 1 && 0 <= l && l <= 1 && k + l <= 1 && 0 <= d && d <= 1)
            {
                bRet = true;
            }
        }
    }
    catch (Exception ex)
    {
        MessageBox.Show(ex.ToString(), "エラー", MessageBoxButtons.OK, MessageBoxIcon.Exclamation);
        bRet = false;
    }
    return bRet;
}

/// <summary>
/// 三角形と直線の交差座標を取得
/// </summary>
/// <param name="vA"></param>
/// <param name="vB"></param>
/// <param name="vC"></param>
/// <param name="vD"></param>
/// <param name="vE"></param>
/// <returns></returns>
private static Vector3 GetCrossPointTriAndLine(Vector3 vA, Vector3 vB, Vector3 vC, Vector3 vD, Vector3 vE)
{
    Vector3 vRet = new Vector3();
    try
    {
        float[] fAry = GetCrossJudgeParam(vA, vB, vC, vD, vE);
        float k = fAry[0];
        float l = fAry[1];
        float d = fAry[2];
        if (0 <= k && k <= 1 && 0 <= l && l <= 1 && k + l <= 1 && 0 <= d && d <= 1)
        {
            Vector3 vAB = vB - vA;
            Vector3 vAC = vC - vA;

            Vector3 vABk = vAB * k;
            Vector3 vACl = vAC * l;
            vRet = vA + vABk + vACl;
        }
    }
    catch (Exception ex)
    {
        MessageBox.Show(ex.ToString(), "エラー", MessageBoxButtons.OK, MessageBoxIcon.Exclamation);
    }
    return vRet;
}

/// <summary>
/// 三角形と線分の交差判定の パラメータ(k,l,d)を取得
/// </summary>
/// <param name="vA"></param>
/// <param name="vB"></param>
/// <param name="vC"></param>
/// <param name="vD"></param>
/// <param name="vE"></param>
/// <returns></returns>
private static float[] GetCrossJudgeParam(Vector3 vA, Vector3 vB, Vector3 vC, Vector3 vD, Vector3 vE)
{
    float[] fAryPram = null;
    try
    {
        // ベクトル
        Vector3 vAB = vB - vA;
        Vector3 vAC = vC - vA;
        Vector3 vDE = vE - vD;
        Vector3 vAE = vE - vA;

        // 連立方程式の左辺の係数を2次元配列に格納
        float[,] fLeft = new float[3, 3];
        fLeft[0, 0] = vAB.X;
        fLeft[0, 1] = vAC.X;
        fLeft[0, 2] = vDE.X;
        fLeft[1, 0] = vAB.Y;
        fLeft[1, 1] = vAC.Y;
        fLeft[1, 2] = vDE.Y;
        fLeft[2, 0] = vAB.Z;
        fLeft[2, 1] = vAC.Z;
        fLeft[2, 2] = vDE.Z;

        // 連立方程式の右辺の値を配列に格納
        float[] fRight = new float[3];
        fRight[0] = vAE.X;
        fRight[1] = vAE.Y;
        fRight[2] = vAE.Z;

        fAryPram = Cramer(fLeft, fRight);
    }
    catch (Exception ex)
    {
        MessageBox.Show(ex.ToString(), "エラー", MessageBoxButtons.OK, MessageBoxIcon.Exclamation);
        fAryPram = null;
    }
    return fAryPram;
}

/// <summary>
/// <para>クラメルの公式 3x3</para>
/// <para>以下のような連立方程式のx,y,zの値が取得できる</para>
/// <para>  2x - 2y + 3z = 7</para>
/// <para>  3x + 2y - 4z = -5</para>
/// <para>  4x - 3y + 2z = 4</para>
/// <para>  答え: x=1, y=2, z=3</para>
/// <para>  引数 a=左辺の係数の二次元配列, b=右辺の値の配列</para>
/// </summary>
/// <param name="a"></param>
/// <param name="b"></param>
/// <returns></returns>
private static float[] Cramer(float[,] a, float[] b)
{
    float[] x = null;
    try
    {
        float detA = det(a);
        if (detA == 0.0)
        {
            return null;
        }
        x = new float[3];
        for (int ii = 0; ii < 3; ii++)
        {
            float[,] a2 = new float[3, 3];
            for (int i = 0; i < 3; i++)
            {
                for (int j = 0; j < 3; j++)
                {
                    if (j == ii)
                    {
                        a2[i, j] = b[i];
                    }
                    else
                    {
                        a2[i, j] = a[i, j];
                    }
                }
            }
            x[ii] = det(a2) / detA;
        }
    }
    catch (Exception ex)
    {
        MessageBox.Show(ex.ToString(), "エラー", MessageBoxButtons.OK, MessageBoxIcon.Exclamation);
        x = null;
    }
    return x;
}

/// <summary>
/// クラメルの公式
/// </summary>
/// <param name="a"></param>
/// <returns></returns>
private static float det(float[,] a)
{
    float a1 = a[0, 0] * (a[1, 1] * a[2, 2] - a[1, 2] * a[2, 1]);
    float a2 = a[0, 1] * (a[1, 2] * a[2, 0] - a[1, 0] * a[2, 2]);
    float a3 = a[0, 2] * (a[1, 0] * a[2, 1] - a[1, 1] * a[2, 0]);
    return a1 + a2 + a3;
}

実行結果

結果①

3D空間上での三角形と直線の交差判定 結果①

結果②

3D空間上での三角形と直線の交差判定 結果②

参考：
http://took.blog72.fc2.com/blog-entry-700.html

コメント

タイトルとURLをコピーしました